6389. Strahler order
In geology, a river system
can be represent as a direct graph. Each river segment is an edge; with the
edge pointing the same way the waters flows. Nodes are either the source of a
river segment (for example, a lake or spring), where rivers segments merge of
diverge, or the mouth of the river.
The Strahler order of
a river system is computed as follows.
·
The order of each source node is 1.
·
For every other node, let i be the highest order of all its upstream
nodes. If just one upstream node has order i, then this node also has order i. If two or more upstream nodes have order i, then this node has order i + 1.
The order of the entire
river system is the order of the mouth node. In this problem, the river system
will have just one mouth. In the picture above, The Strahler order is
three (3).
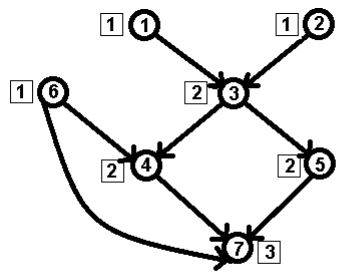
The number in a box is the
order. The number in a circle is the node number.
You must write a program to
determine the order of a given river system.
The actual river with the
highest order is the Amazon, with order 12. The highest in the U.S.
is the Mississippi, width order 10.
Input. The first line contains the number t
(1 ≤ t ≤ 1000) of
data sets that follow. Each data set should be processed independently.
Each data set consists of
multiple lines. The first line of each data set contains three positive
integers k, m and p (2
≤ m ≤ 1000). k is the data set
number. m is the number of
nodes in the graph and p is
the number of edges. The first line is followed by p lines, each describing an
edge of the graph. The line will contain two positive integers a and b, indicating that water
flows from node a to
node b (1 ≤ a, b
≤ m). Node m is the mouth of the river. It has no outgoing
edges.
Output. For each data set there is
a single line of output. The line consists o the data set number, a single
space and the order of the river system.
|
Sample input |
Sample output |
|
1 1 7 8 1 3 2 3 6 4 3 4 3 5 6 7 5 7 4 7 |
1 3 |
SOLUTION
graphs – depth
first search
Algorithm analysis
Construct a directed graph with reverse edges. The mouth of the original graph will be the source of the constructed
one, and from it we’ll run the depth first search. In the process of searching, we recompute the Strahler
order order[v] for each vertex v as
described in the problem statement.
Consider the vertex v. Let to1, to2, …, tok
be its sons. We need to know the greatest Strahler order among the sons,
as well as the number of times it occurs among them. Let the structure map<int,int> mp; stores the
pairs (order, cnt) – the Shtraler order and the
number of times it occurs among the sons.
For example, vertex 7
has three sons:
·
vertex 6 with Strahler order 1;
·
vertex 4 with
Strahler order 2;
·
vertex 5 with Strahler order 2;
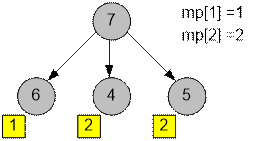
Vertex 7 among
its sons has:
·
one vertex with Strahler
order
1, so mp[1]
= 1;
·
two vertices with Strahler order 2, so mp[2] = 2;
Find the maximum Strahler order among the sons of the vertex v.
·
if it occurs only in one son to, set order[v] = order[to];
·
if it occurs in more that one son, set order[v] = order[to] + 1;
For the vertex 7 the
maximum Strahler order is 2, it is achieved at two vertices: 4 and 5. So order[7] = order[4]
+ 1 = 2 + 1 = 3.
Algorithm realization
The
reverse graph is constructed in the
adjacency list g. In order[i] we’ll compute the Strahler order for the i-th vertex.
vector<vector<int>
> g;
vector<int>
order;
Function dfs runs depth first search
from the vertex v and returnes the Strahler
order for the vertex v.
int dfs(int v)
{
If the Strahler
order is already computed for the vertex v, return it.
if (order[v] > 0) return
order[v];
Iterate
over the sons to of the vertex v. We must find the greatest Strahler order among the sons, as
well as the number of times it occurs among them. In the structure mp, we store
the pairs (order, cnt) – the Strahler order and the number of times it occurs among the sons to.
int suns = 0, mx = 0;
map<int,int> mp;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i];
mp[dfs(to)]++;
}
If vertex v (v is a leaf) has no sons, then its Strahler order is 1.
if (mp.empty())
order[v] = 1;
else
{
Set the
iterator iter to the pair with the maximum Strahler order.
map<int,int>::iterator
iter = mp.end();
iter--;
If
the maximum order is achieved at only one son, then the order of v equals to the
order of that son.
if ((*iter).second == 1)
order[v] = (*iter).first;
else
Otherwise,
the order of v equals to the order of this son, increased by 1.
order[v] = (*iter).first + 1;
}
return order[v];
}
The main part of the program. Read the input data. Construct a
reverse graph. For each original edge u → v, add an edge v →
u to our graph.
scanf("%d",
&tests);
for(i = 1; i
<= tests; i++)
{
scanf("%d %d %d",&k,&m,&p);
g.clear(); g.resize(m + 1);
order.clear(); order.resize(m + 1);
for(j = 1; j <= p; j++)
{
scanf("%d %d",&u,&v);
g[v].push_back(u);
}
Run the depth
first search from the mouth of the river
– the vertex m
and print its Strahler order with the test
number.
res =
dfs(m);
printf("%d %d\n",i,res);
}